Heap 堆

[TOC]

1、优先队列

​ 数组实现

​ 插入：元素插入尾部 ​ 删除：遍历找到最大或最小，删除，然后移动原素。

​ 链表实现

​ 插入：元素插入头部或尾部 ​ 删除：遍历找到最大或最小，删除。

​ 搜索二叉树

​ 插入：元素插入。 =》平衡？ ​ 删除：遍历找到最大或最小，删除。 =》平衡？

​ 完全二叉树

​ 重新构建一种树，专注于插入和删除最大或最小。即，根节点总是最大或最小且结构满足完全二叉

​ 树。满足这种结构的树称为堆。

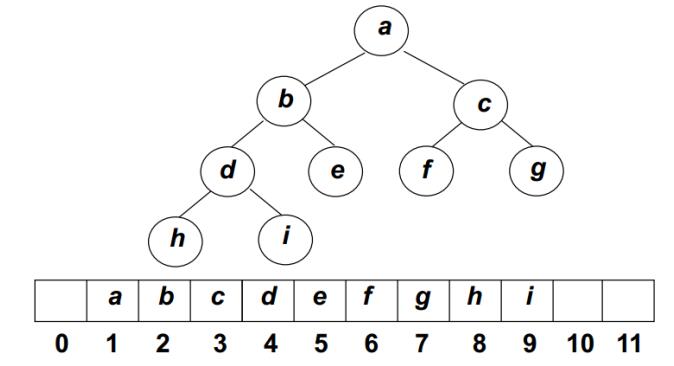
特点：

​ 结构性：用数组表示完全二叉树。

​ 有序性：任一节点的关键字是其子树所有节点的最值（最大或最小）。最大值者，称为最大堆；“最大堆（MaxHeap）”，也称 “ 大顶堆”。 “ 最小堆（MinHeap） ”，也称“ 小顶堆 ”。

​ 下标性：

​ 当 i=1 时，该结点为根结点，它无双亲结点；

​ 当 i>1 时，其双亲是结点 i/2 (“/”表示整除)； ​ 若 2i≤n，则第 i 个结点有编号为 2i 的左孩子； ​ 若 2i+1≤n，则第 i 个结点有编号为 2i+1 的右孩子

最大堆

​ 插入

​ 最大堆的插入操作可以简单看成是“结点上浮”。当我们在向最大堆中插入一个结点我们必须满足完

​ 全二叉树的标准，那么被插入结点的位置的是固定的。而且要满足父结点关键字值不小于子结点

​ 关键字值，那么我们就需要去移动父结点和子结点的相互位置关系。

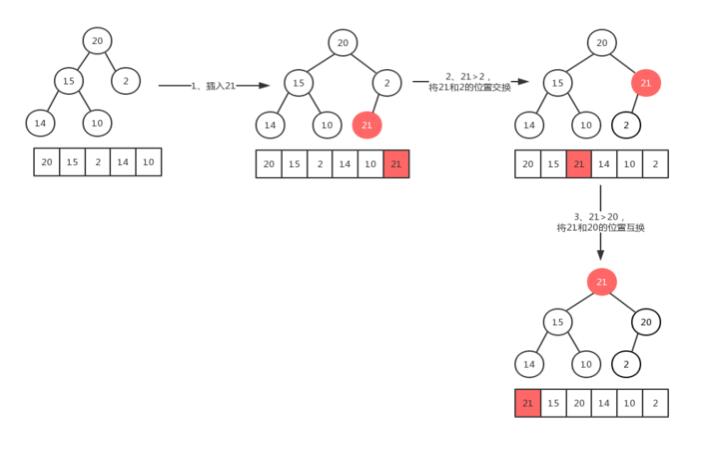
​ 删除

​ 最大堆的删除操作，总是从堆的根结点删除元素。同样根元素被删除之后为了能够保证该树还是

​ 一个完全二叉树，我们需要来移动完全二叉树的最后一个结点，让其继续符合完全二叉树的定义，从这里可以看作是最大堆最后一个结点的下沉。

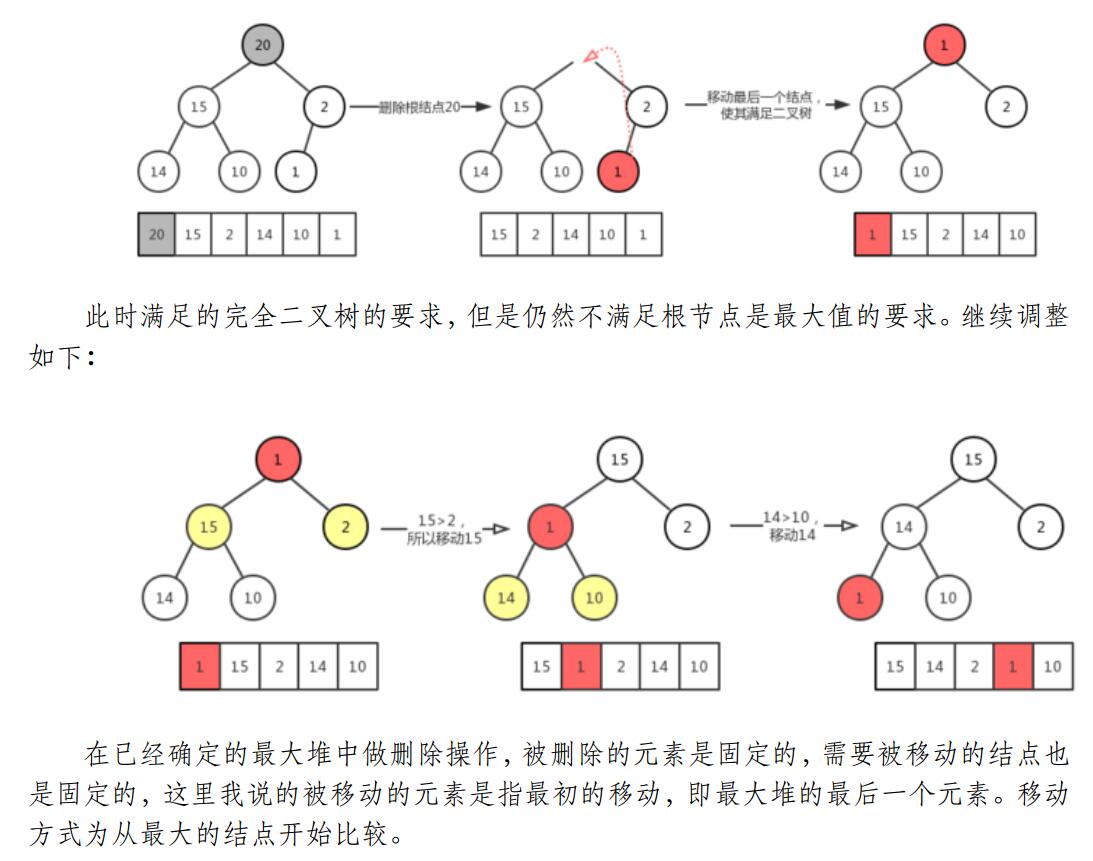
代码实现：

heap.h

#ifndef  __HEAP_H__
#define  __HEAP_H__

typedef struct _MaxHeap
{
	int *_space;
	int _size;
	int _capcity;

}MaxHeap;

MaxHeap * createMaxHeap(int msize);
int isMaxHeapFull(MaxHeap *h);
int isMaxHeapEmpty(MaxHeap *h);
void insertMaxHeap(MaxHeap *h, int data);
int deleteMaxHeap(MaxHeap *h);

#endif

实现

heap.cpp

#include"Heap.h"
#include<stdio.h>
#include<stdlib.h>

MaxHeap * createMaxHeap(int msize)
{
	MaxHeap *Head = (MaxHeap *)malloc(sizeof(MaxHeap));
	Head->_space = (int *)malloc(sizeof(int)*(msize + 1));
	Head->_size = 0;
	Head->_capcity = msize;
	return Head;

}
int isMaxHeapFull(MaxHeap *h)
{
	if (h->_size + 1 == h->_capcity)
		return 1;
	else
		return 0;
}
int isMaxHeapEmpty(MaxHeap *h)
{
	return h->_size == 0;
}
void insertMaxHeap(MaxHeap *h, int data)
{
	int i;
	if (!isMaxHeapFull(h))
	{
		i = ++h->_size;
		for (; data > h->_space[i / 2] && i>1; i /= 2)
			h->_space[i] = h->_space[i / 2];
		h->_space[i] = data;
	}
}
int deleteMaxHeap(MaxHeap *h)
{
	if (isMaxHeapEmpty(h))
	{
		printf("Head is empty  ");
		return -1;
	}
	int parent, child;
	int max, t;

	max = h->_space[1];
	t = h->_space[h->_size--];

	for (parent = 1; parent * 2 <= h->_size; parent = child)
	{
		child = parent * 2;//左儿子
						   //判断存不存在右儿子，如果有右儿子，左右儿子，谁大
		if (child != h->_size && h->_space[child] < h->_space[child + 1])
			child++;
		if (t >= h->_space[child])
			break;
		else
			h->_space[parent] = h->_space[child];
	}
	h->_space[parent] = t;
	return max;

}

main.c

#include"Heap.h"
#include<stdio.h>
#include<stdlib.h>

int main()
{
	int msize = 10;
	MaxHeap *Head=createMaxHeap(msize+1);
	
	int a = isMaxHeapFull(Head);
	printf("  %d  \n", a);

	insertMaxHeap(Head, 1);
	insertMaxHeap(Head, 3);
	insertMaxHeap(Head, 5);
	insertMaxHeap(Head, 7);
	insertMaxHeap(Head, 9);
	insertMaxHeap(Head, 2);
	insertMaxHeap(Head, 4);
	insertMaxHeap(Head, 6);
	insertMaxHeap(Head, 8);
	insertMaxHeap(Head, 10);
	
	int b = isMaxHeapEmpty(Head);
	printf("  %d  \n", b);

	for (int i=1; i < msize+1; i ++ )
	{
		printf("  %d  ", Head->_space[i]);
	}
	return 0;
}

最小堆

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

//vector                         arr
//list                           doublelist
//dequeue
//stack   queue
//
//priority_queue                 heap

//map                            ab
//unorder_map   hash_map         hash

void dis(vector<int> &vi)
{
    for(auto &i:vi)
    cout<<i<<" ";
    cout<<endl;

}



int main()
{
    int arr[10]={1,3,5,7,9,2,4,6,8,10};

    vector<int > vi(arr,arr+10);

     make_heap(vi.begin(),vi.end());  //最大堆
   dis(vi);


    make_heap(vi.begin(),vi.end(),greater<int>()); //最小堆
    dis(vi);

//    vi.push_back(100);
//    make_heap(vi.begin(),vi.end(),greater<int>());
//    dis(vi);

//    pop_heap(vi.begin(),vi.end(),greater<int>());
//    dis(vi);


//     sort_heap(vi.begin(),vi.end());
//     dis(vi);
    sort_heap(vi.begin(),vi.end(),greater<int>());
    dis(vi);
    return 0;
}