04Tree

tree 树

对于查找来说 分为两类。

​ 一、数据体量不变的，称为静态查找 （线性 和二分法）

​ 二、数据体量可以动态的扩容和缩减。需要动态查找。（二分查找搜索树）

学习路线：

​ 森林 ---> 树 ---> 二叉树 ---> 搜索二叉树 ---> 平衡搜索二叉树

​ 树(Tree) : n(n≥0)个结点构成的有限集合。当 n=0 时，称为空树；对于任一棵非空树(n≥0)，它具备以下性质： ​ 树中有一个称为"根(Root)"的特殊结点，没有父节点； ​ 其余结点可分为 m(m>0)个互不相交的有限集 T1， T2， ... ， Tm，其中每个集 ​ 合本身又是一棵树，称为原来树的"子树"(SubTree)。 注：树的定义具有递归性，即"树中还有树",仅有一个根结点的树是最小树。

​ 树的深度( Depth) ：树中所有结点中的最大层次是这棵树的深度。

二叉树

二叉树是 n(n≥0)个结点的有限集合。n=0 的树称为空二叉树；n>0 的二叉树由一个根结点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成，左、右子树也是二叉树，所以子树也可以为空树。

基本特征:

​ ① 每个结点最多只有两棵子树(不存在度大于 2 的结点)；( 度 就是 树叉) ​ ② 二叉树的子树，有左右之分，左子树和右子树次序不能颠倒。所以下面是两棵不同的树。

满二叉树： 在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子结点都在同一层上，这样的二叉树称为满二叉树。

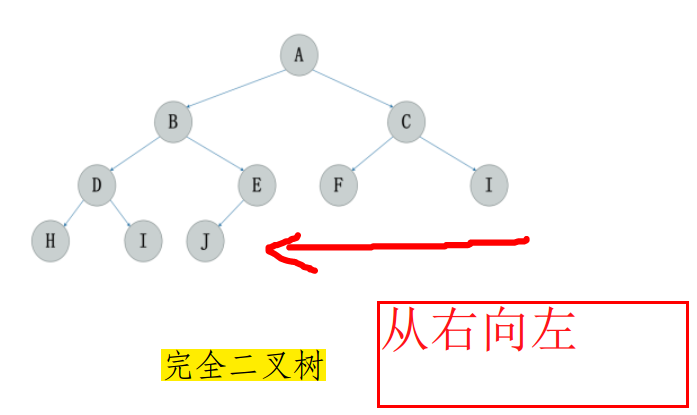
完全二叉树： 如果一棵深度为 k，有 n 个结点的二叉树中各结点能够与深度为 k 的顺序编号的满二叉树从 1 到 n 标号的结点相对应的二叉树称为完全二叉树。

二叉树的存储

​ 线性存储一般仅用于满二叉树和完全二叉树。

​

链式存储

1、递归实现

​ 前序遍历 中序遍历 后序遍历

​ 1.访问根节点 1.中序遍历左子树 1.后序遍历左子树

​ 2.前序遍历左子树 2.访问根节点 2.后序遍历右子树

​ 3.前序遍历右子树 3.中序遍历右子树 3.访问根节点

#include<stdio.h>

typedef struct TreeNode
{
public:
	int _data;
	struct  TreeNode *_left;
	struct  TreeNode *_right;
}TreeNode;

void preOrderTraverase(TreeNode *r)        //前序遍历
{
	if (r)
	{
		printf("%d  ",r->_data);
		preOrderTraverase(r->_left);
		preOrderTraverase(r->_right);
	}
}

void midOrderTraverase(TreeNode *r)        //中序遍历
{
	if (r)
	{
		midOrderTraverase(r->_left);
		printf("%d  ", r->_data);
		midOrderTraverase(r->_right);
	}
}

void postOrderTraverase(TreeNode *r)      //后序遍历
{
	if (r)
	{
		postOrderTraverase(r->_left);
		postOrderTraverase(r->_right);
		printf("%d  ", r->_data);
	}
}

int getHeightByPostOrder(TreeNode *t)
{
	int lH, rH, maxH;

	if (t)
	{
		lH = getHeightByPostOrder(t->_left);
		rH = getHeightByPostOrder(t->_right);
		maxH = (lH > rH) ? lH : rH;
		return maxH + 1;
	}
	else
		return 0;
}

int main()
{
	TreeNode a, b, c, d, e, f;
	TreeNode * root = &a;
	
	a._data = 1; b._data = 2; c._data = 3;
	d._data = 4; e._data = 5; f._data = 6;

	a._left = &b;   a._right = &c;
	b._left = &d;   b._right = &e;
	c._left = nullptr; c._right = &f;

	d._left = d._right = e._left = e._right = f._left = f._right = nullptr;

	  // preOrderTraverase(root);  
	  // putchar(10);
	  //midOrderTraverase(root);
	  //putchar(10);
	  postOrderTraverase(root);
	  putchar(10);
	  
	  int high= getHeightByPostOrder(root);
	  printf("\n  high = %d  \n\n", high);
	   return 0;
}

2、循环实现

非递归算法实现的基本思路：使用栈

递归的方式，每一个节点有 3 次访问的机会，但是对于压栈来说，每个压入的节 点，只有 2 次访问的机会。

mystack.h

#ifndef MYSTACK_H
#define MYSTACK_H

typedef struct _TreeNode
{
public:
	int _data;
	struct  _TreeNode *_left;
	struct  _TreeNode *_right;
}TreeNode;

typedef struct _Stack
{
	int _len;
	int _top;
	TreeNode **_space;  //游标
}Stack;

void initStack(Stack *s,TreeNode* size);

int isStackFull(Stack *s);
int isStackEmpty(Stack *s);

void push(Stack *s, TreeNode* ch);

TreeNode* pop(Stack *s);
void clearStack(Stack *s);
void resetSatck(Stack *s);
#endif // MYSTACK_H

实现 stack.cpp

#include"myStack.h"
#include<stdlib.h>

void initStack(Stack *s,TreeNode* size)
{
	s->_top = 0;
	//s->_len = size;
	s->_space = (TreeNode **)malloc(sizeof(TreeNode));
}

int isStackFull(Stack *s)
{
	//    if(s->_top==s->_len)
	//        return true;
	//    else
	//        return false;

	return s->_top == s->_len;
}

int isStackEmpty(Stack *s)
{
	return s->_top == 0;
}

void push(Stack *s, TreeNode* ch)
{
	s->_space[s->_top++] = ch;
}

TreeNode* pop(Stack *s)
{
	return s->_space[--s->_top];
}

void clearStack(Stack *s)  //清空   销毁栈
{
	free(s->_space);
}

void resetSatck(Stack *s)
{
	s->_top = 0;
}

main.cpp

#include<stdio.h>
#include"myStack.h"


void preOrderTraverase(TreeNode *r)        //前序遍历
{
	if(r)
	{
		Stack s;
		initStack(&s,r);
		while (r || !isStackEmpty(&s))//t 为空，但是栈内不空
		{
			while (r)
			{
				printf("%d  ", r->_data);/*(访问)结点*/
				push(&s, r);
				r = r->_left; /*一直向左并将沿途结点压入堆栈*/
			}
			if (!isStackEmpty(&s))
			{
				r = pop(&s); /*结点弹出堆栈*/
				r = r->_right; /*转向右子树*/
			}
		}
	}
}

void midOrderTraverase(TreeNode *r)    //中序遍历
{
	if (r)
	{
		Stack s;
		initStack(&s,r);
		while (r || !isStackEmpty(&s))
		{
			while (r)
			{
				push(&s, r);
				r = r->_left;
			}
			if (!isStackEmpty(&s))
			{
				r = pop(&s);
				printf("%d  ", r->_data);
				r = r->_right;
			}
		}
	}
}

void  postOrderTraverase(TreeNode *r)     //后序遍历
{
	Stack s;
	initStack(&s, r);
	TreeNode *cur;
	TreeNode *pre = nullptr;
	push(&s, r);
	while (!isStackEmpty(&s))
	{
		cur = pop(&s);
		push(&s, cur);

		if ((cur->_left == nullptr && cur->_right == nullptr) ||
			(pre != nullptr && (pre == cur->_left || pre == cur->_right)))
		{
			//如果当前结点没有孩子结点或者孩子节点都已被访问过
			printf("%d  ", cur->_data);
			pop(&s);
			pre = cur;
		}
		else
		{
			if (cur->_right != nullptr)
				push(&s, cur->_right);
			if (cur->_left != nullptr)
				push(&s, cur->_left);
		}
	}
}


int main()
{
	TreeNode a, b, c, d, e, f;
	TreeNode * root = &a;

	a._data = 1; b._data = 2; c._data = 3;
	d._data = 4; e._data = 5; f._data = 6;

	a._left = &b;   a._right = &c;
	b._left = &d;   b._right = &e;
	c._left = nullptr; c._right = &f;

	d._left = d._right = e._left = e._right = f._left = f._right = nullptr;

	 preOrderTraverase(root);  
	 putchar(10);
	 midOrderTraverase(root);
	 putchar(10);
	
	 postOrderTraverase(root);
	 putchar(10);

	return 0;
}