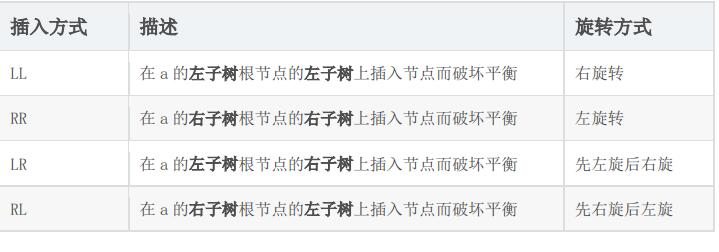
06Tree-sbt

平衡搜索二叉树 (平衡二叉树)

重要性 影响树的平衡的因素主要有，插入顺序，删除节点。一旦树失去了平衡性，其查找效率就会下降，甚至失去查找效率。

常见的平衡手段 AVL Tree和 RB Tree

AVL Tree

必要的条件：

条件一：它必须是二叉查找树。

条件二：每个节点的左子树和右子树的高度差至多为 1。 (黄色节点不满足)

1、失衡

平衡因子(BF)：将二叉树上节点的左子树高度减去右子树高度的值称为该节点的平衡因子BF(Balance Factor)。

对于平衡二叉树，BF的取值范围为**[-1,1]**。如果发现某个节点的 BF 值不在此范围，则需要对树进行调整。

最小不平衡子树

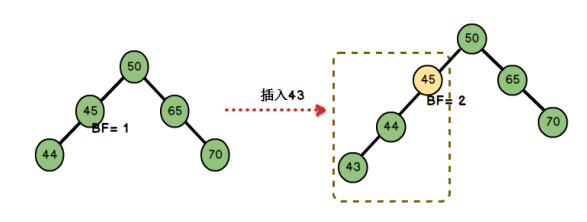
左边二叉树的节点 45 的 BF = 1，插入节点 43 后，节点 45 的 BF = 2。节点 45是距离插入点 43 最近的 BF 不在[-1,1]范围内的节点，因此以节点 45 为根的子树为最小不平衡子树。

2、平衡

节点的插入或删除都有可能导致 AVL 树失去平衡，因此，失衡调整是插入与删除操作的基础。调节的宗旨是，消灭不平衡因子，且是搜索二叉树。 AVL 树的失衡调整可以分为四种情况：

a、 左单旋(RR)

当我们在右子树插入右孩子导致 AVL 失衡时，我们需要进行单左旋调整。旋转围绕最小失衡子树的根

节点进行。在删除新节点时也有可能会出现需要单左旋的情况。

b、右单旋(LL)

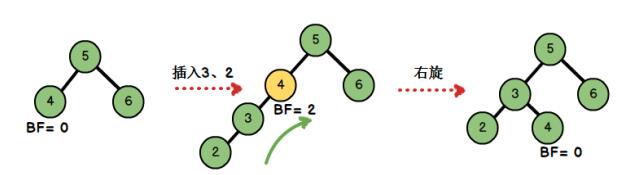
插入 3、 2 后出现了不平衡的情况。此时的插入情况是“在左子树上插入左孩子导致 AVL 树失衡”，我

们需要进行单右旋调整。

c、右左双旋(RL)

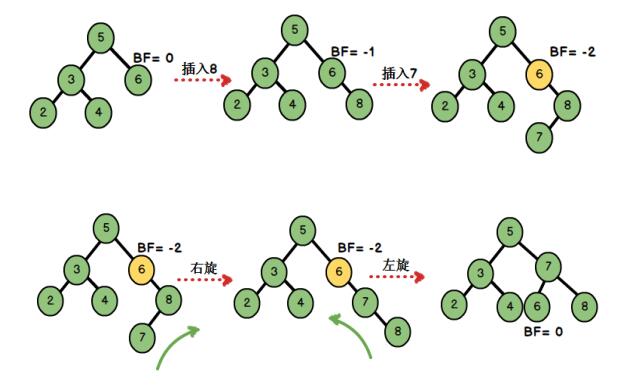
需要进行两次旋转的原因是第一次旋转后， AVL 树仍旧处于不平衡的状态，第二次旋转再次进行调

整。这种情况，总结起来就是“在右子树上插入左孩子导致 AVL 树失衡",此时我们需要进行先右旋后左

旋的调整。

d、左右双旋

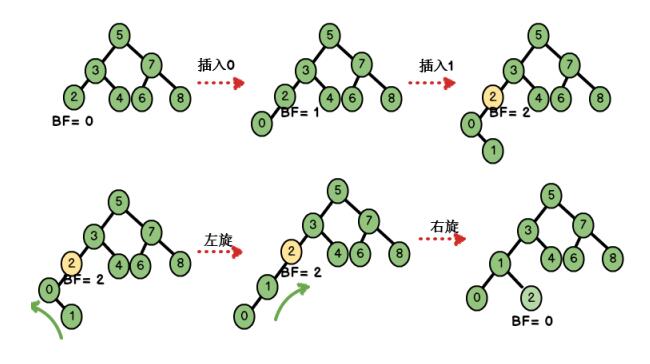
根据对称性原理，当我们“在左子树上插入右孩子导致 AVL 树失衡",此时我们需要进行先左旋后右旋的

调整。

旋转小节